1319 连通网络的操作次数

标签: 并查集

题目

题目链接：1319 连通网络的操作次数

用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b。

网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。

给你这个计算机网络的初始布线 connections，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。 

示例 1：

输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。

示例 2：

输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
输出：2

提示：

1 <= n <= 10^5
1 <= connections.length <= min(n*(n-1)/2, 10^5)
connections[i].length == 2
0 <= connections[i][0], connections[i][1] < n
connections[i][0] != connections[i][1]
没有重复的连接。
两台计算机不会通过多条线缆连接。

思路

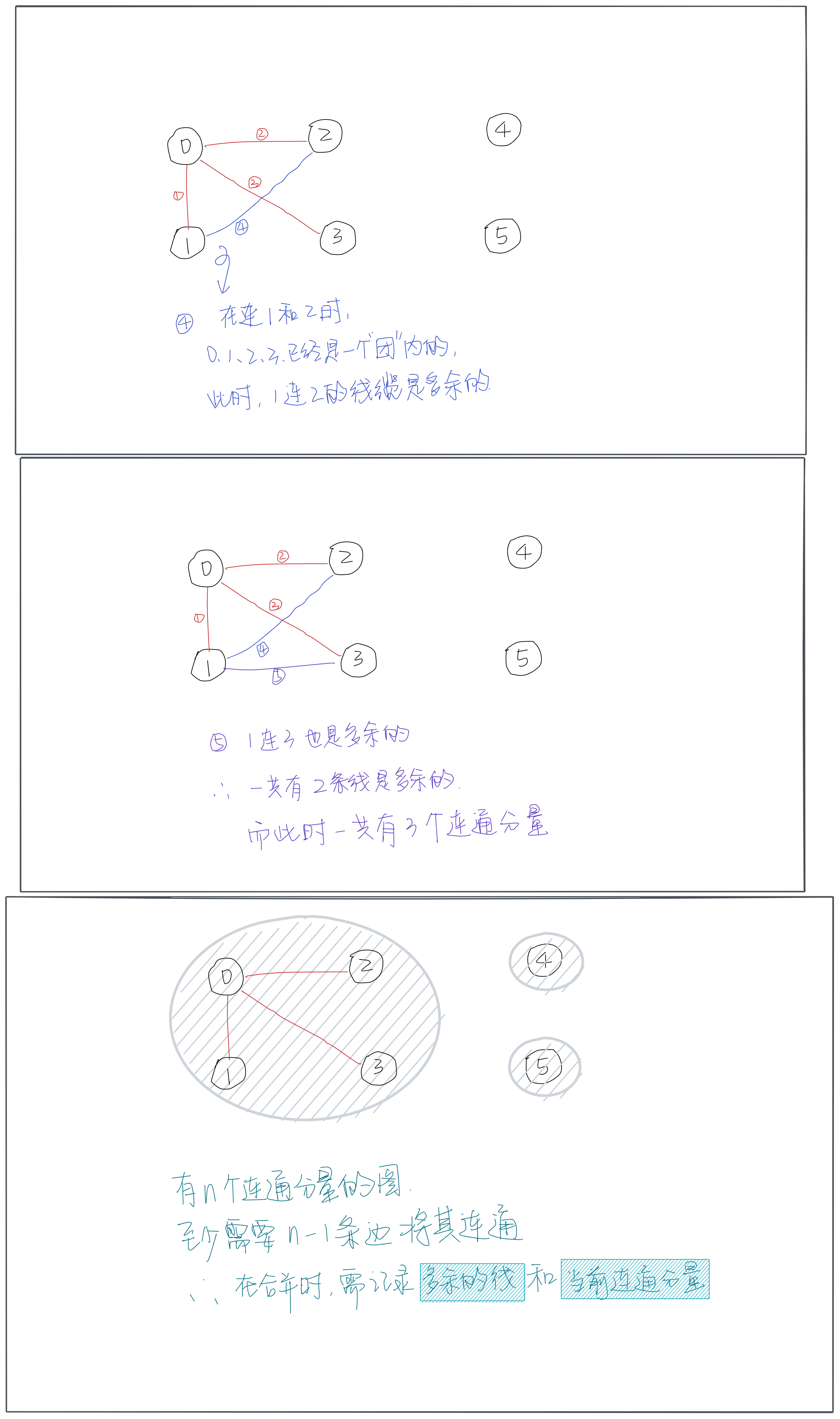
代码

class Solution:
    def makeConnected(self, n: int, connections: List[List[int]]) -> int:
        def find(p):
            while p != self.parent[p]:
                p = self.parent[p]
            return p
        
        def union(p,q):
            # 如果 p 和 q 同属于一个团，就不必连接了
            # 否则，会影响连通分量的计数
            if connect(p, q): return 
            leader_p = find(p)
            leader_q = find(q)
            self.parent[leader_p] = leader_q
            # 每连接一次，连通分量就 -1
            self.cnt -= 1
            
        def connect(p, q):
            if find(p) == find(q):
                return True
            return False

        # 初始化
        # 1. 连通分量为节点个数
        self.cnt = n            
        # 2. 并查集指向节点自身
        self.parent = { i : i for i in range(n)}            
        # 3. 多余线缆为 0
        extra = 0               

        for p,q in connections:
            if connect(p, q):
                # 如果已经连通，多余线缆 extra 加一
                extra += 1
                # 就不用再连了
                continue
            union(p, q)

        if extra < self.cnt - 1:
            # 边的条数 < 连通分量 - 1 ，就连不通
            return -1
        
        # 连通分量 - 1
        return self.cnt - 1