279 完全平方数

标签: BFS, 动态规划, 队列

题目

题目链接：279 完全平方数

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

给你一个整数 n ，返回和为 n 的完全平方数的 最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13
输出：2
解释：13 = 4 + 9

提示：

1 <= n <= 104

思路 I

BFS + queue

1. 使用 BFS + 队列 的组合

2. 根节点：n

3. 之后的每层节点：

   1. 上一层节点减去平方数的差。

   2. 这就意味着队列存储的是某一层完整的节点，要么都出队，要么都入队。

   3. 出队的节点可以通过减去各个平方数，得到若干个差，作为新的一层的节点入队。

4. 最终「和为 n 的完全平方数的最少数量」即为节点所在的层数。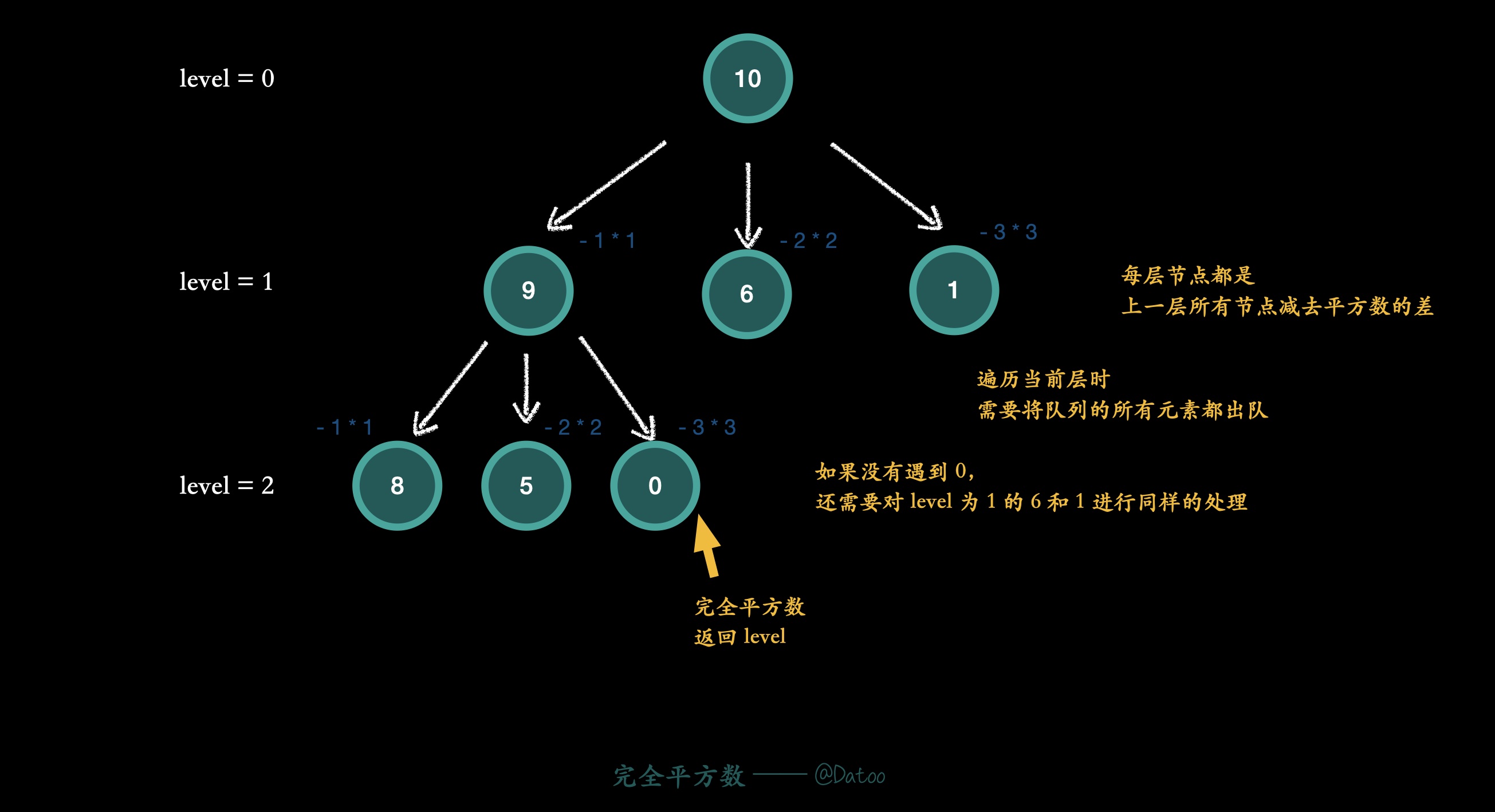

   

代码 I

class Solution:
    def numSquares(self, n: int) -> int:
        import queue
        q = queue.Queue()
        q.put(n)
        level = 0
        visited = set()

        while q.qsize() > 0:
            size = q.qsize()
            level += 1

            # 整层的节点都要出队
            for _ in range(size):
                node = q.get()

                # 用于平方数计数
                s = 1
                while s * s <= node:
                    sub = node - s * s
                    
                    # 找到完全平方数，此时的层数为「和为 `n` 的完全平方数的最少数量」
                    if sub == 0:
                        return level

                    if sub not in visited:
                        visited.add(sub)
                        q.put(sub)

                    s += 1
        return -1

---

思路 II

动态规划

1. 每个元素 i 的完全平方数的最少数量取决于：

   1. 从 1 到 i-1 的完全平方数的最少数量

   2. i 是否为平方数

2. 因此，动态规划的转移方程为：$dp[i] = min(dp[1]+dp[i-1], \ dp[2]+dp[i-2], … )$

3. 这样的思路是可行的，但是会超时。因为求状态转移时，每次都要遍历 $\frac{i}{2}$ 次，时间复杂度为 O(n * n). 如果不用遍历 $[1, i-1]$ 的每一个数，而是遍历 $[1, i-1]$ 的每一个平方数，那么耗时就会好很多。

4. 此时，动态规划的状态转移方程为：$dp[i] = min(dp[i], dp[i - s * s] + 1), s \times s\in [1, i]$

代码 II

class Solution:
    def numSquares(self, n: int) -> int:
        dp = {i : 0  for i in range(0, n+1) }
        dp[1] = 1
        dp[2] = 2

        for cur in range(3, n+1):
            dp[cur] = cur
            s = 1
            while s * s <= cur:
                dp[cur] = min(dp[cur], dp[cur - s * s] + 1)
                s += 1

        return dp[n]