33 搜索旋转排序数组
标签: 二分搜索
题目
题目链接:33. 搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的索引,否则返回 -1 。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
提示:
1 <= nums.length <= 5000
-10^4 <= nums[i] <= 10^4
nums 中的每个值都 独一无二
nums 肯定会在某个点上旋转
-10^4 <= target <= 10^4
进阶:你可以设计一个时间复杂度为 O(log n) 的解决方案吗?
思路
欢迎访问我在 LeetCode 上的题解
本题采用 二分搜索总结 里的「模版 I」实现
- 根据「旋转点」的位置,可分为两种情况:靠左或靠右。 不管怎么旋转,旋转后的数组都有以下特点:
蓝色数组的最小值 > 黄色数组的最大值,即所有蓝色数组的元素 > 所有黄色数组的元素;- 蓝色数组长度和黄色数组长度孰长孰短,是动态变化的,取决于指针的移动。

- 再根据「整体数组的中间值」和「蓝黄长度对比」,
target的落点可分为以下 6 种情况:- 当旋转点靠右时:(
target可落在 ①~③)- 如果
target落在了1区:则nums[mid] > target。因为nums[mid]和target属于同一数组,target更靠左,就更小。 - 如果
target落在了2区:则nums[mid] < target。因为nums[mid]和target属于同一数组,target更靠右,就更大。 - 如果
target落在了3区:则nums[mid] > target。因为nums[mid]属于蓝色数组,target属于黄色数组,并且所有蓝色数组的元素 > 所有黄色数组的元素。
- 如果
- 当旋转点靠左时:(
target可落在 ④~⑥)- 如果
target落在了4区:则nums[mid] < target。因为nums[mid]属于黄色数组,target属于蓝色数组,并且所有黄色数组的元素 > 所有蓝色数组的元素。 - 如果
target落在了5区:则nums[mid] > target。因为nums[mid]和target属于同一数组,target更靠左,就更小。 - 如果
target落在了6区:则nums[mid] < target。因为nums[mid]和target属于同一数组,target更靠右,就更大。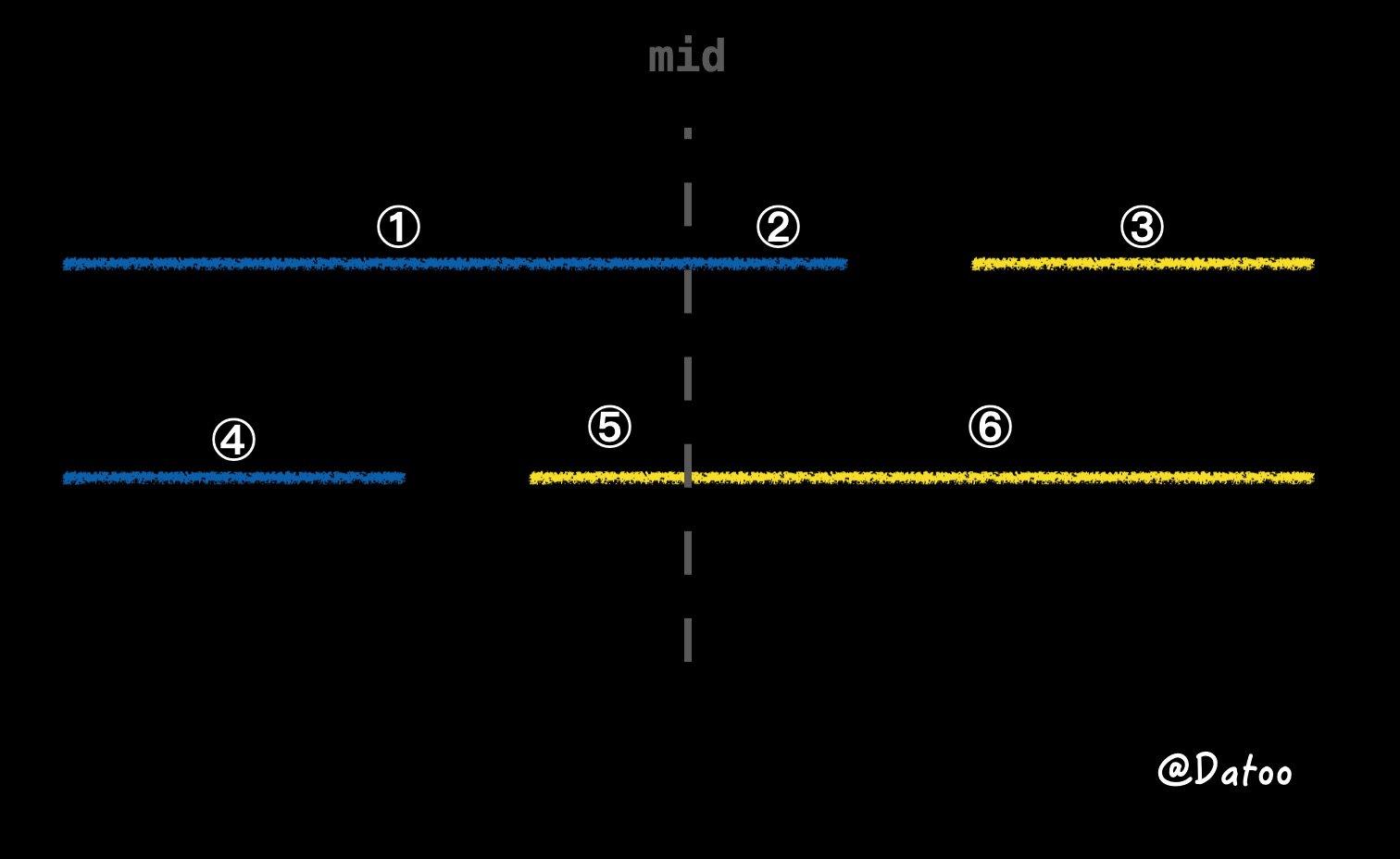
- 如果
- 当旋转点靠右时:(
- 转换为代码的思路:(指针的移动)
- 当旋转点靠右时,如果
target落在了1区,那么右指针 一定会向左移动。只需判断 $target$ 是否处于 $[nums[left], nums[mid]]$ 区间内即可。 - 同理。当旋转点靠左时,如果
target落在了6区,那么左指针 一定会向右移动。只需判断 $target$ 是否处于 $[nums[mid], nums[right]]$ 区间内即可。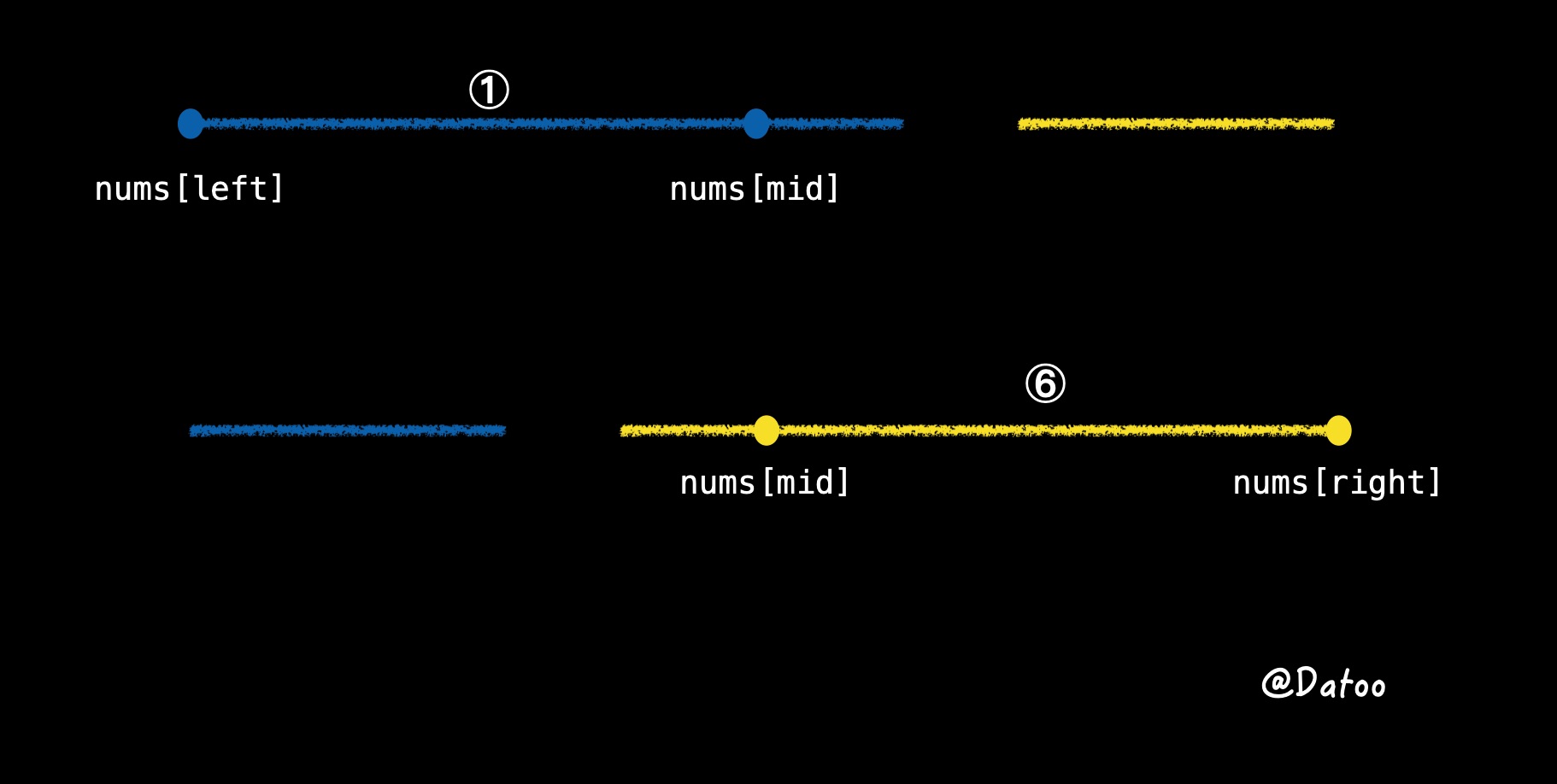
- 当旋转点靠右时,如果
代码
class Solution:
def search(self, nums: List[int], target: int) -> int:
# 初始化
left, right = 0, len(nums)-1
# 终止条件
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
# 旋转点靠右
if nums[mid] >= nums[left]:
# target 落在 1 区
if nums[left] <= target <= nums[mid]:
right = mid - 1
else:
left = mid + 1
# 旋转点靠左
else:
# target 落在 6 区
if nums[mid] <= target <= nums[right]:
left = mid + 1
else:
right = mid - 1
return -1
分析
使用二分搜索可将复杂度降为 O(log n)

留下评论