树总结

标签: 总结, 树

树的基本信息

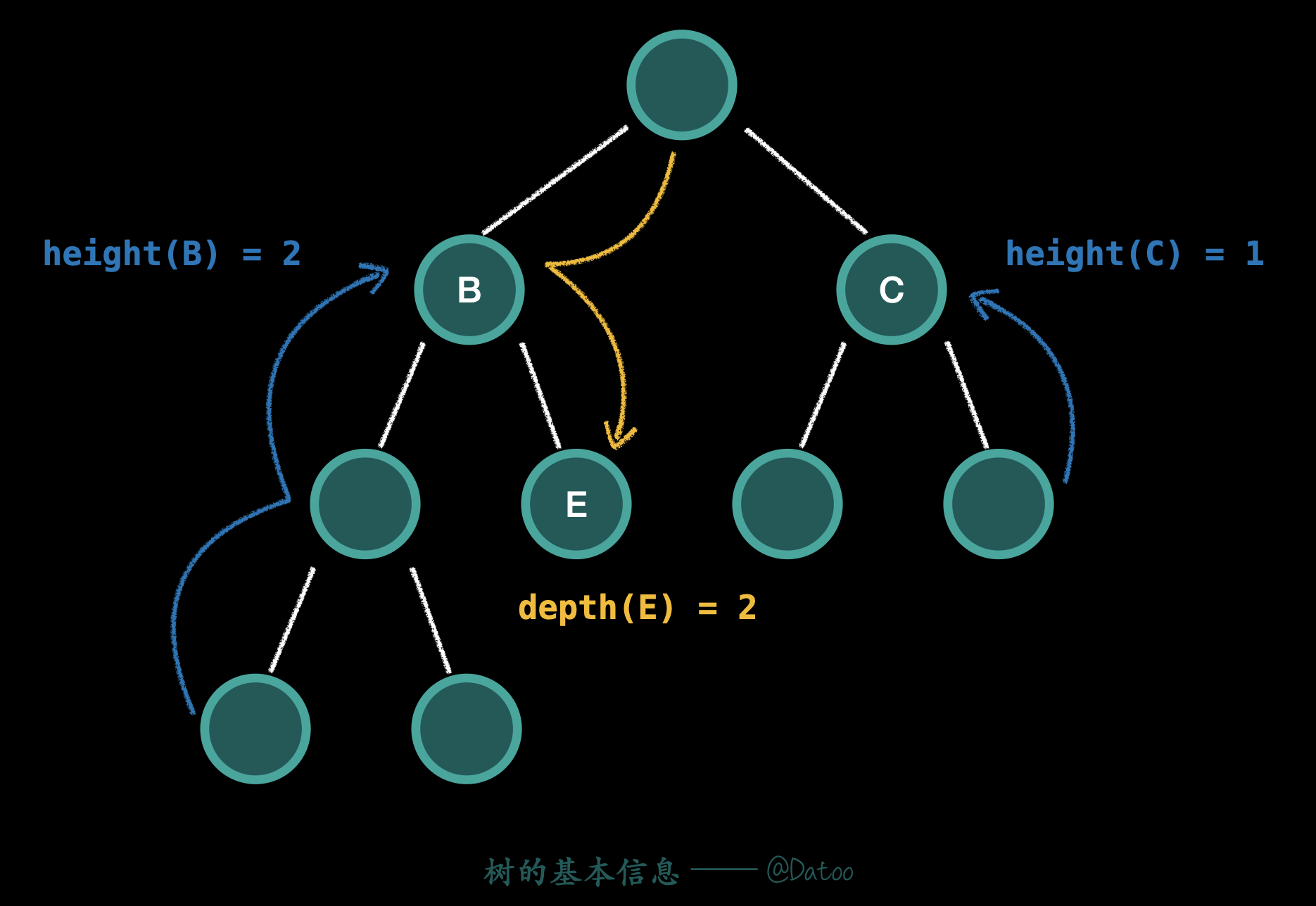
• 树的高度：从下往上，叶子节点到节点的路径

• 树的深度：从上到下，根节点到节点的路径

• 

二叉树分类

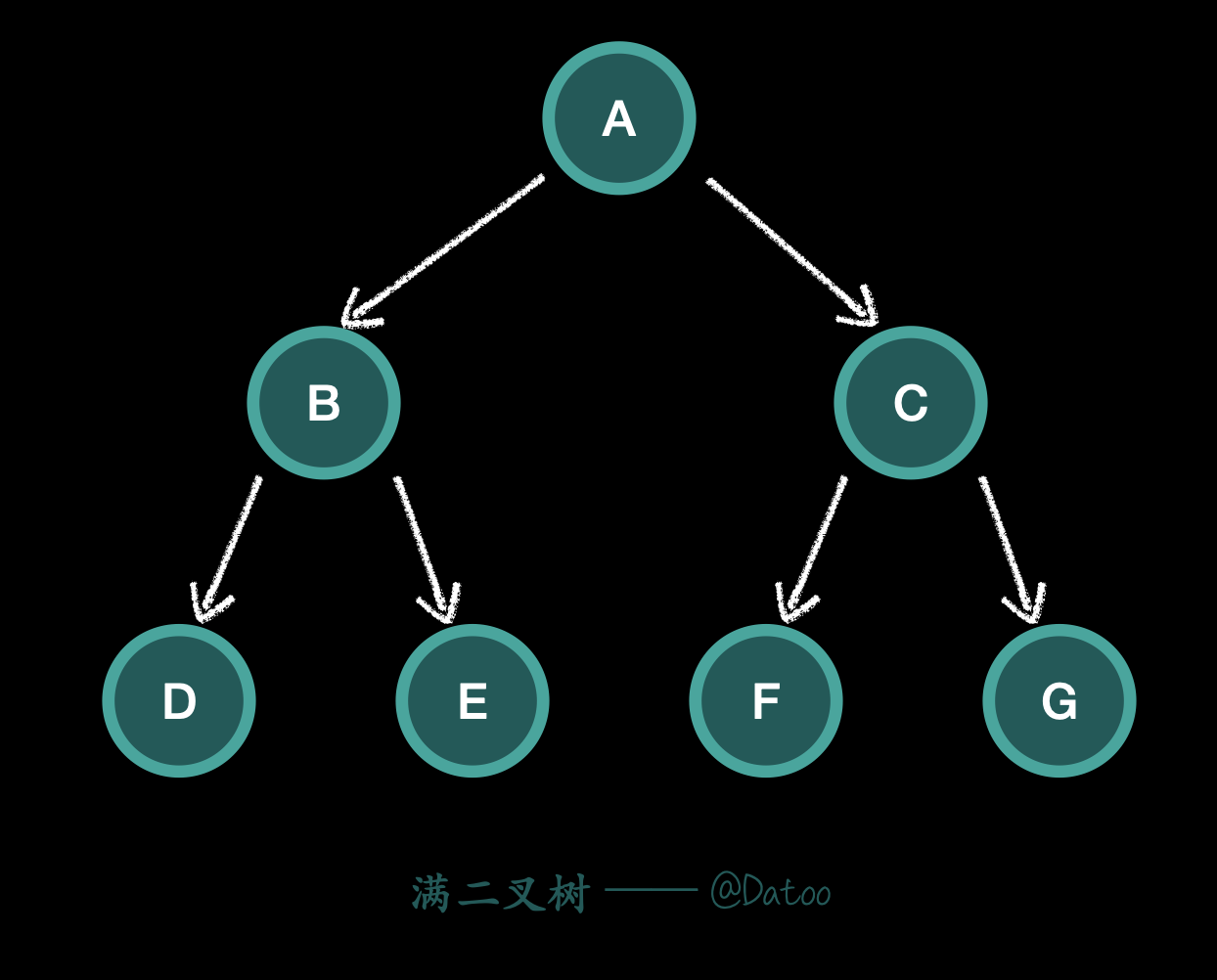
满二叉树

• 高度为 $h$ ，由 $2^h - 1$ 个节点构成的二叉树称为满二叉树。

• 

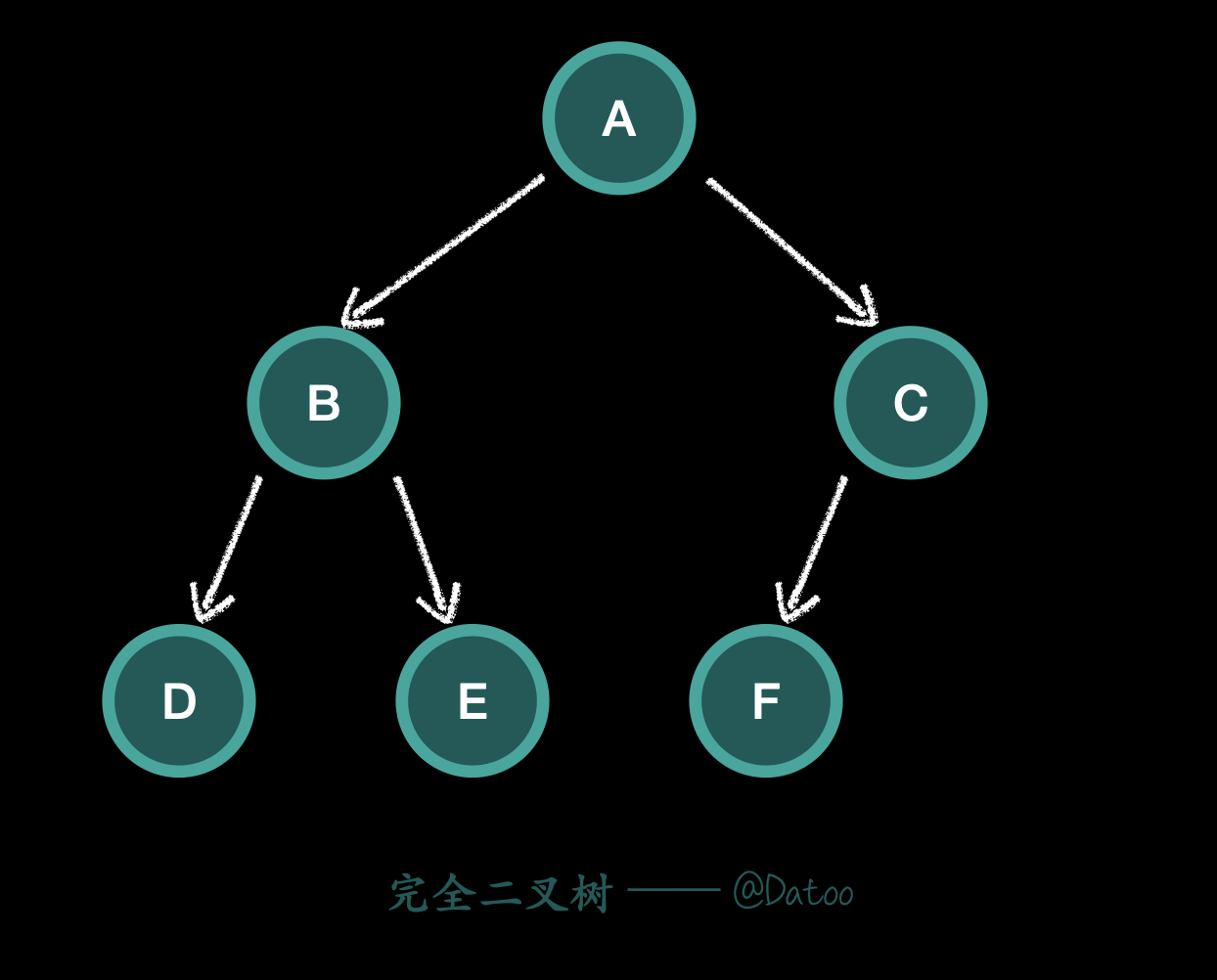
完全二叉树

• 在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。

• 可以理解为，在满二叉树的基础上，最后一层没填满的二叉树。或第 $1$ 至 $h-1$ 层都为满二叉树。

• 若最底层为第 $h$ 层，则该层包含 $[1, 2(h-1)]$ 个节点。

• 

堆

• 一般用 完全二叉树 来实现；

• 通常以 数组 的形式存储；

• 堆 to 数组：当前元素索引为 i
  • 如果索引从 0 开始：左孩子为 2i+1 ，右孩子为 2i+2 ，父节点为 (i-1)/2
  • 如果索引从 1 开始：左孩子为 2i ，右孩子为 2i+1 ，父节点为 i//2
• 分类：
  • 最大堆：A[parent] >= A[children]
  • 最小堆：A[parent] <= A[children]
• 应用：堆排序、topk问题、作业调度（优先队列）

二叉搜索树

• 性质：$左孩子 < 根节点, 右孩子 > 根节点$，不含等号；

• 二叉搜索树的中序遍历结果是一个有序列表；

• 最好的情况下，是 O(logn)，此时二叉排序树的查找效率比较高，近似于二分查找；

• 最差的情况下，是 O(n)，比如插入的元素是有序的，生成的二叉排序树就是一个链表，此时需要遍历全部元素。因此需要平衡二叉树来平衡一下。

平衡二叉树

• 据维基百科：一般的二叉查找树的查询复杂度取决于目标结点到树根的距离（即深度），因此当结点的深度普遍较大时，查询的均摊复杂度会上升。为了实现更高效的查询，产生了平衡树。在这里，平衡指所有叶子的深度趋于平衡，更广义的是指在树上所有可能查找的均摊复杂度偏低。

• 平衡二叉树的特点：

  • 平衡二叉树要么是一棵空树

  • 要么保证左右子树的高度之差不大于 1

  • 子树也必须是一颗平衡二叉树

• 参考：3 分钟理解完全二叉树、平衡二叉树、二叉查找树

• 相关题目：

  No	Problem	Difficulty	Link	Solution	Comment
  110	平衡二叉树	简单	题目	题解	有助于对平衡二叉树的特点进行了解
  剑指offer 55	平衡二叉树	简单	题目	题解	与上题相同
  108	将有序数组转换为二叉搜索树	简单	题目	题解	对二叉搜索树的特点进行了解，并对二分法加以使用
  109	有序链表转换二叉搜索树	中等	题目	题解	与上题 108 类似，对链表进行二分，构造二叉搜索树
  1382	将二叉搜索树变平衡	中等	题目	题解	对二叉搜索树的特点的利用，将问题转换为 108 题

树的遍历方式

1. 深度优先（DFS）

LeetCode上的超级大户 🤣

1. 分为「前」、「中」、「后」序遍历；

2. 借助「栈」；

3. 适合暴力枚举的题目；

4. 如果借助函数调用栈，可以使用递归实现。

5. 对性能有很高要求时，用迭代；其他时候，用递归。

2. 广度优先（BFS）

1. 分为「带层」和「不带层」；

2. 借助「队列」；

3. 适合求「最短距离」：BFS 核心价值在于，求「最短问题」可以提前终止，而 DFS 需要穷举所有可能才能找到最近的。

4. 不是「层次遍历」：层次遍历不需要提前终止，是 BFS 的副产物。