并查集总结

标签: 并查集, 总结

一、介绍

1. 是什么

1. 英文：Disjoint-set data structure 或 Union-find data structure
2. 直译：「没有交集的数据结构」或「联合-查找数据结构」
3. 本质上，是一种图结构。这种图的特点可以用 “不交集森林(Disjoin-set forest)” 概括：将集合当作是一棵树，在森林中，有许多这样的树（集合）并且它们之间没有交集。
4. 表示：
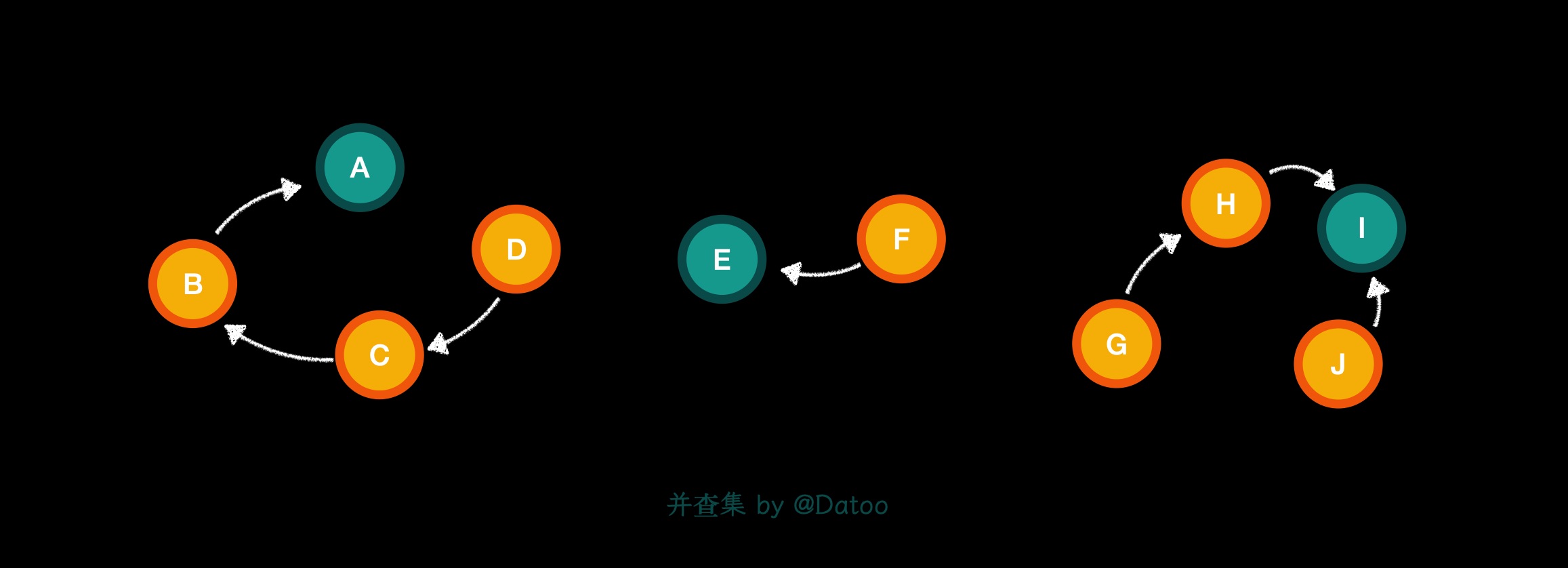
   1. 每个集合用一棵树表示，每个元素用每个节点表示；
   2. 树的每个节点（图中橙色节点）都保存着它的父节点；
   3. 树的根节点（图中绿色节点）则保存一个空引用或者到自身的引用或者其他无效值，以表示自身为根节点。

2. 可以做什么

支持一系列没有重复元素的集合的 查询和合并 操作

1. 查询：返回待查询元素所属的 集合的代表元素。主要用于判断两个元素是否同属于一个集合。如上图：
   1. 查找节点 D，返回其所在树（集合）的代表元素 A；
   2. 查找节点 G，返回其所在树（集合）的代表元素 I；
   3. 查找节点 B，返回其所在树（集合）的代表元素 A；
   4. 节点 D 和 B 因为代表元素相同，则同属于一颗树；而节点 G 在另一个棵树里。
2. 合并：将两个集合合并为一个集合。

3. 并查集的优化

3.1 路径压缩

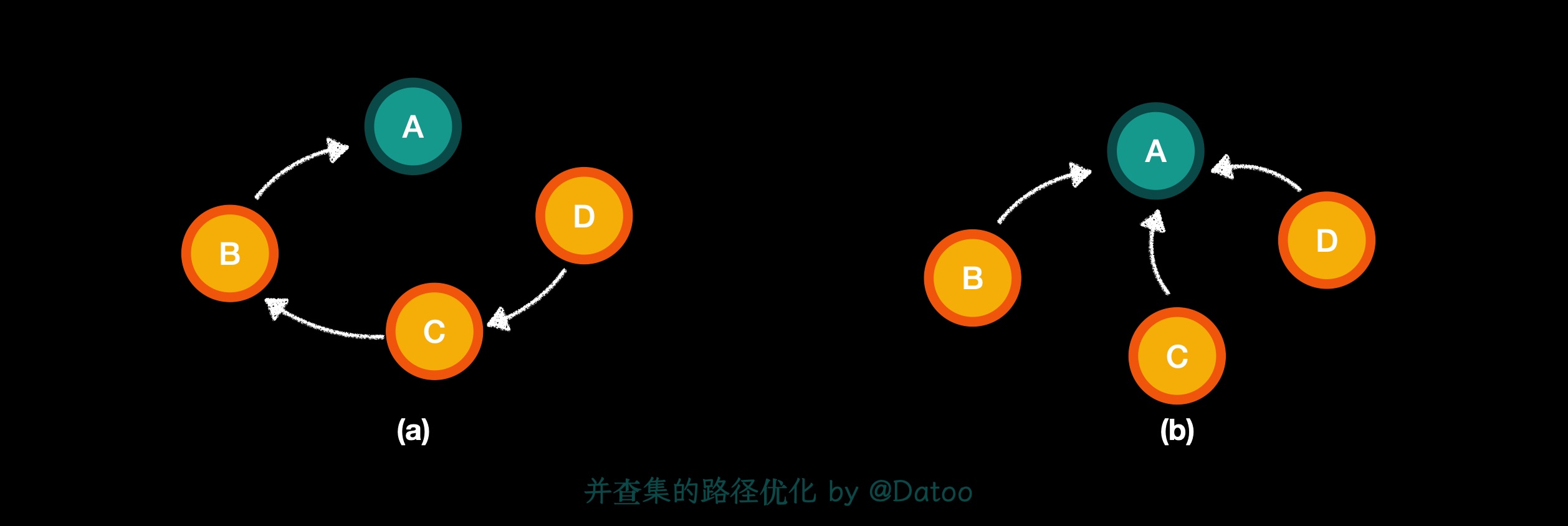
1. 如图(a)：当在集合很大或者树很不平衡时，树就变成了「一颗线性树」，单次查询的时间复杂度高达 ${\displaystyle \mathrm {O} \left(n\right)}$。

2. 如图(b)：一个常见的优化是路径压缩：在查询时，把被查询的节点到根节点的路径上的所有节点的父节点设置为根结点，从而减小树的高度。也就是说，在向上查询的同时，把在路径上的每个节点都直接连接到根上，以后查询时就能直接查询到根节点。

3.2 按秩合并

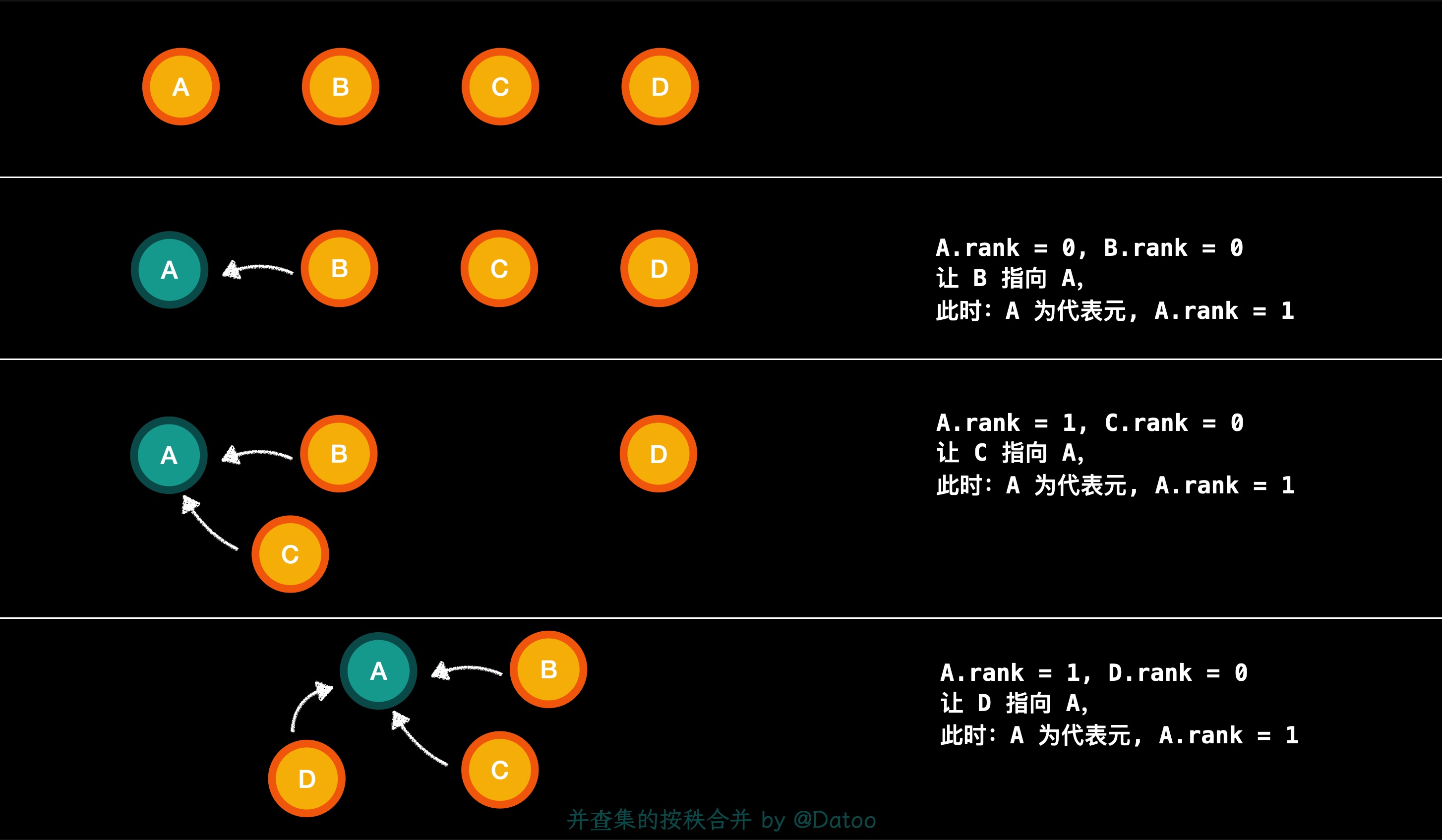
1. 秩：指节点的高度。
2. 按秩合并：将较小秩的根指向较大秩的根（与路径压缩稍微不同的是，此处是合并两棵树，路径压缩是添加元素的优化策略）。

二、模版

1. 不带优化

1.1 节点数据

class UF:
    def __init__(self, M):
        # 初始化 parent 和 cnt
        self.parent = {}
        self.cnt = 0

1.2 查找

1. 代表元的特点：其父元素等于其自身。
2. 步骤：循环查找节点的父元素，直到抵达其自身为父元素的元素，即为代表元。

    def find(self, x):
        while x != self.parent[x]:
            x = self.parent[x]
        return x

1.3 合并

1. 步骤：
   1. 合并之前先判断两个节点是否同属于一个集合，self.connnected()；
   2. 分别找到两个节点所在集合的代表元，将其中一个代表元指向另一个代表元。

def union(self, p, q):
    if self.connected(p, q): return
    self.parent[self.find(p)] = self.find(q)
    self.cnt -= 1

def connected(self, p, q):
    return self.find(p) == self.find(q)

1.4 整个模版

class UF:
    def __init__(self, M):
        # 初始化 parent 和 cnt
        parent = {}
        cnt = 0

    def find(self, x):
        while x != self.parent[x]:
            x = self.parent[x]
        return x
    
    def union(self, p, q):
        if self.connected(p, q): return
        self.parent[self.find(p)] = self.find(q)
        self.cnt -= 1
    
    def connected(self, p, q):
        return self.find(p) == self.find(q)

2. 带优化

2.1 节点数据

class UF:
    def __init__(self, M):
        # 初始化 parent，size 和 cnt
        parent = {}
        size = {}
        cnt = 0

2.2 查找

1. 如前所述，路径压缩的做法是：在向上查询的同时，把在路径上的每个节点都直接连接到根上，以后查询时就能直接查询到根节点。

def find(self, x):
    while x != self.parent[x]:
        x = self.parent[x]
        # 路径压缩：
        # 找到 x 的爷爷节点 self.parent[self.parent[x]], 令其存储为 x 的父节点
        # 之后查询时，能够缩短查询的路径
        self.parent[x] = self.parent[self.parent[x]]
    return x

2.3 合并

1. 步骤：
   1. 合并之前先判断两个节点是否同属于一个集合，self.connnected()；
   2. 分别找到两个节点所在集合的代表元；
   3. 得到两个代表元的秩，将秩小的代表元指向秩大的代表元。

def union(self, p, q):
    # 是否同属于一个集合
    if self.connected(p, q): return

    # 找到两个节点的代表元
    leader_p = self.find(p)
    leader_q = self.find(q)

    # 将秩小的树挂到秩大的树上， 使树尽量平衡
    if self.size[leader_p] < self.size[leader_q]:
        self.parent[leader_p] = leader_q
        self.size[leader_q] += self.size[leader_p]
    else:
        self.parent[leader_q] = leader_p
        self.size[leader_p] += self.size[leader_q]

    self.cnt -= 1

def connected(self, p, q):
    return self.find(p) == self.find(q)

2.4 整个模版

class UF:
    parent = {}
    size = {}
    cnt = 0
    def __init__(self, M):
        # 初始化 parent，size 和 cnt

    def find(self, x):
        while x != self.parent[x]:
            x = self.parent[x]
            self.parent[x] = self.parent[self.parent[x]]
        return x

    def union(self, p, q):
        if self.connected(p, q): return

        leader_p = self.find(p)
        leader_q = self.find(q)
        
        if self.size[leader_p] < self.size[leader_q]:
            self.parent[leader_p] = leader_q
            self.size[leader_q] += self.size[leader_p]
        else:
            self.parent[leader_q] = leader_p
            self.size[leader_p] += self.size[leader_q]
        self.cnt -= 1

    def connected(self, p, q):
        return self.find(p) == self.find(q)

三、应用

1. 确定无向图的连通分量

2. 亲戚问题，是否同个祖先

3. 检测图是否有环

四、相关题目

No	Problem	Difficulty	Link	Solution	Comment
1319	连通网络的操作次数	中等	题目	题解	并查集的基础应用